Probabilism II – Ramsey’s Sure-Loss Bets

Is it rational to take a bet you’re guaranteed to lose? Suppose you even knew that there was no way of winning. Would knowingly taking a sure-loss bet be a rational thing to do? Of course not! Unless there is some kind of overall good you are aiming for, or the circumstances are very unusual, agreeing to a guaranteed loss is dumb move. Most of us would see it as irrational behavior. And as it turns out, anyone who so much as violates one of Kolmogorov’s Axioms is doing exactly that: agreeing to a sure loss. This marks perhaps one of the most powerful arguments for Probabilism. Why think Probabilists are right that anyone who breaks their rules are irrational? Because if an agent does so, she will accept bets she is guaranteed to lose, and surely that is irrational. At least, that’s what we will try and give an informal proof for later on. But first, let’s talk about gambling.

The fact that these rule-breaking agents will accept such bets was first pointed out by mathematician and philosopher Frank Ramsey. In his words, “These are the laws of probability, which we have proved to be necessarily true of any consistent set of degrees of belief,” and anyone who broke these laws “could have a book made against him by a cunning better and would then stand to lose in any event” (22).¹ Books of the devious sort Ramsey describes have come to be known as “Dutch Books.” (It is debated where the name comes. One theory has it that in the 19^th century, Dutch insurance companies for ships would combine insurances in such a way as to make money no matter what contingency occurred. True or not, this story gets the idea across.)² To understand how these books represent a sure loss for violating agents, first consider the ticket below for some proposition P:

If you are rational, how much would you pay for this ticket? The answer, Titlebaum explains, hinges on “how confident you are that P is true […] A ticket that pays off on P is worth more to a rational agent the more confident she is of P.”² If an agent is confident P is false, she will think the ticket is likely worthless. She won’t pay much for it unless she thinks there is a reasonable chance P is true.⁴ For example, suppose P is the proposition that a fair coin will come up tails. An agent, knowing the coin is fair, can be 50% confident that P. Given that the ticket entitles her to $1 if P is true, her fair betting price is then $0.50. By paying this amount for the ticket, she stands to gain net $0.50 should the coin comes up tails, and to lose $0.50 should the coin comes up heads. This strikes most of us as a fair bet. We can express these two outcomes in the form of a table. Assuming the agent has paid her fair betting price of $0.50, we can write the payoffs where P is true or false as:

Consider a similar example: the proposition that a balanced six-sided die will roll six. Call this proposition R. R has a 1/6 likelihood of being true. Suppose an agent believes the die is balanced, and so her fair betting price for a ticket paying off $1 if R is true is one sixth of a dollar, or $0.16̅6. By betting this amount, she is risking no more than she believes the odds warrant. Put a more familiar way, she risks no more than her credence that the die will roll six. This brings us to what we will call the Fair Betting Price Principle, or the FBPP: An agent’s fair betting price for any proposition P will always equal her cr(P).¹ (This assumes, of course, that an agent’s stakes are expressed in the same real number range as her credences, in our case [0,1].) Similarly, an agent’s fair selling price for any proposition P will also equal her cr(P). This is just to say that if a person will spend 1/6 of a dollar on a ticket that pays $1 if a fair die rolls six, then she will also sell that ticket for 1/6 of a dollar to someone else, where if the die rolls six, she has to pay them $1. Her stakes are the same in either case. Titelbaum sums this up by saying, “In general, an agent’s fair betting price for a gambling ticket is both the maximum amount she would pay for that ticket and the minimum amount for which she would sell it.”³ The important thing to remember here is this: An agent’s cr(P) is the fair price for which she would both buy and sell a ticket paying out $1 on P. That’s the Fair Betting Price Principle. An agent’s fair betting price will always equal her credence.

Right off the bat, there is a subtle but important fact to notice about this principle, and it is this: The FBPP says an agent’s fair betting price is equal to her credence that P is true, not the actual probability that P is true. If her credence about the truth of P is accurate, then these two numbers will be the same. But often enough, we believe claims to be more or less likely true than they really are. The actual likelihood of something is not the same thing as someone’s estimate of what that likelihood is, and estimates can be wrong. So, there is a difference between betting prices which are objectively fair and those which are merely believed to be fair. We will call the latter kind “subjectively fair” betting prices. Because the FBPP involves an agent’s credence, it is a principle about subjectively fair betting prices. The purpose of the FBPP is to describe the conditions under which an agent has no reason to think a bet is unfair, not the conditions under which a bet really is fair or not. And if an agent has no reason to think a bet is unfair, then all things being equal, she will take it.

Dutch Book Theorem

With the FBPP in hand, we may start to wonder what sort of bets would be accepted by agents with unusual credence values – in particular, agents whose credences violate Kolmogorov’s Axioms or any of their corollaries. What kinds of bets might someone agree to if their credences failed to satisfy the axiom of Non-negativity, for example? In 1937, Italian statistician Bruno de Finetti was thinking about exactly these questions, and he managed to prove what Ramsey had suspected years prior: That if an agent violates any one of the probability axioms, they will agree to a sequence of one or more bets which have only losing outcomes for the agent.⁴ This result has come to be known as the Dutch Book Theorem. Recall that a “Dutch Book” is defined as any sure-loss set of bets. And in most thought experiments involving Dutch Books, hypothetical “Dutch bookies” are the clever opportunists who construct them. (Again, who knows if probability theorists had something against the Dutch, but whatever the etymology, the name has stuck.) The fact that violating agents would willingly accept a sure loss from Dutch bookies, Probabilists argue, should surely strike us as irrational. This is the thrust of the so-called Dutch Book argument for Probabilism.

An informal proof for the Dutch Book Theorem is easy enough. All we have to do is build three Dutch Books, each one for agents who violate a different Kolmogorov’s Axiom. It can be quite satisfying to see how the bets work together. Sometimes it only takes a single bet to secure a sure loss. You’ll see what I mean with this first one.

Dutch Book for Normality: Suppose your confidence in tautologies is greater than %100. Then, using the tautology P or ~P, a Dutch bookie could sell you the following ticket:

Since your credence that cr(P or ~P) > 1, then by the FBPP your fair betting price $B is also > $1. So for more than a dollar, you will happily buy a ticket paying off $1 if P is true. Since the bet is on a tautology, you are guaranteed to receive $1 as the holder. A guaranteed $1 sounds great! So, what is the problem then? Remember, you paid $B to enter the bet, which is an amount greater than $1. The prize will not be enough for you to break even, let alone make a profit. By paying $B > $1 to receive $1, you have effectively lost $(B – 1). This is the only possible outcome. No matter what happens, you face a sure loss and the bookie a sure gain.² Likewise, if the situation is different, and your credence in a tautology is less than 1 rather than greater, a similar fate awaits. The same ticket can be bought from you to guarantee you a sure loss as well.⁶ Thus, an agent is only safe from this Dutch Book if they satisfy the Normality Axiom, and have credence of exactly 1 for tautologies.

Dutch Book for Non-negativity: If an agent has a confidence level below zero for some proposition P, they are violating the axiom of non-negativity. These people are not just committing a doxastic taboo. They are also making themselves vulnerable to a dangerous bet.⁴ Suppose your credence that P is true is less than zero, or put more mathy, your cr(P) < 0. Then, given the FBPP, your fair betting price equals your cr(P). For this negative price, you would buy a ticket paying out $1 if P is true. You would also sell such a ticket at this price too. If we let $S represent your fair selling price, then that means $S equals cr(P). And since cr(P) < 0, it is also true $S < $0. This means that when you are selling someone (say, Dutch bookie) a ticket, you will sell at your negative betting price of $S. A Dutch bookie will be paying a negative price for this ticket, and so that bookie will be given money ($S) by you to become the holder. And since the ticket rewards $1 to the holder if P is true, there is no way to make your money back. Its game over! If P is false, you will gain nothing and you are still out by $S. And if P turns out to be true, you will only be giving the bookie more money – a further $1! Either way, you lose and the bookie profits. We can describe the situation from your perspective with the table below.³

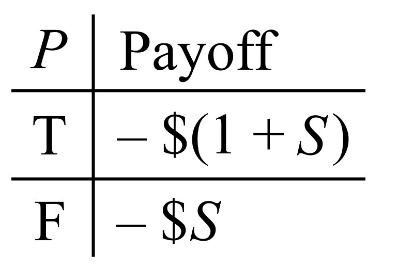
Dutch Book for Finite Additivity: Suppose that for some mutually exclusive propositions P and Q, your sureness that either P or Q is true is less than your sureness that P and Q are true put together. That is, your credences are such that cr(P or Q) < cr(P) + cr(Q). Suppose also your credence values are cr(P) = 0.5, cr(Q) = 0.5, and cr(P ∨ Q) = 0.2. Since these values are also your fair betting prices on each proposition, a Dutch bookie need only do two things to ensure a profit. First, the bookie sells you a pair of tickets: one for $0.50 that rewards $1 if P, and another for $0.50 that rewards $1 if Q. Next, the bookie buys a ticket from you for $0.20 that rewards $1 if (P ∨ Q).

What is the result of these exchanges? For starters, you have paid $0.50 twice for your two tickets, and sold one ticket for $0.20. So far, you have lost a total of $0.80. You are not empty handed, however. You still have your two tickets and will win $1 if either P or Q is true. Since P and Q are mutually exclusive, though, there is no way for both tickets to win. At most, you stand to gain $1. But therein lies the catch: If either P or Q is true, and you do gain $1, then so will the bookie! Recall that you sold a ticket of your own to the bookie which pays $1 to the holder if (P or Q) is true. Either P or Q cannot be true without (P or Q) also being true, of course. This means that there is no outcome in which you gain $1 from one of your two tickets without also having to pay that $1 right back to the bookie. Thus, you can never make back the $0.80 you lost in the beginning. Even if neither P or Q are true and you keep the $0.20 from the bookie, it is still the case that you paid a total of $1 for your two tickets, neither of which would win in this case. Thus, you are sure to lose $0.80 in every outcome. Your grim situation is shown in the table below, where the ticket columns represent your net total for each ticket, and the rightmost column represents the grand total of every ticket.^{3, 4}

The mutual exclusivity of P and Q means there is no possible outcome P and Q, so it is not included in the table. For the similar situation where you have credence cr(P or Q) greater than cr(P) + cr(Q), the bookie need only reverse the direction of these bets to guarantee you a sure loss.

After pulling off this very informal proof, the conclusion we come to is this: If an agent flouts any of Kolmogorov’s Axioms, they are endangering themselves to Dutch bookies. By constructing a set of sure-loss bets agreeable to violators of each axiom, we can create a Dutch Book for anyone whose credences do not play by the Probabilists’ rules.⁴ This is a powerful argument that Probabilists have in their arsenal. It is also, I should admit, my personal favorite.

Comments